Cách tính tọa độ hình chiếu vuông góc của điểm lên mặt phẳng

Hình chiếu vuông góc của điểm lên mặt phẳng là một khái niệm trong hình học không gian dùng để xác định tọa độ hình chiếu của một điểm lên mặt phẳng.

Hình chiếu vuông góc của điểm lên mặt phẳng được tính bằng cách xác định vị trí điểm H trên mặt phẳng dựa trên tọa độ và hướng vuông góc với đường thẳng AH.

Hãy cùng Mosflyvn tìm hiểu khái niệm hình chiếu vuông góc của một điểm lên mặt phẳng và cách tính tọa độ hình chiếu chính xác nhất.

Khái niệm hình chiếu vuông góc của điểm lên mặt phẳng

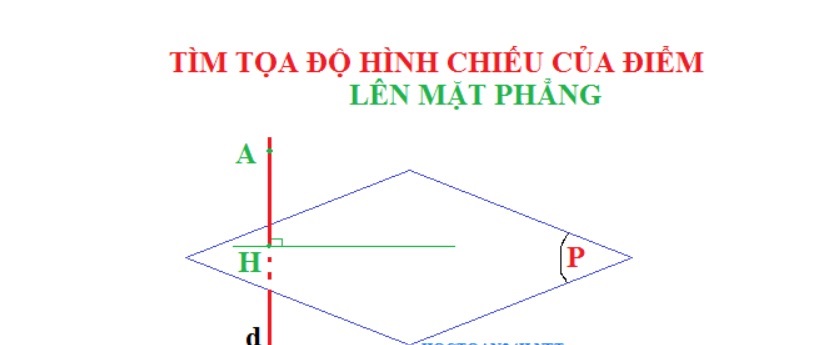
Hình chiếu vuông góc của một điểm lên mặt phẳng.

Hình chiếu vuông góc của một điểm lên mặt phẳng là duy nhất, là điểm chính giữa của đoạn thẳng nối điểm đó với chân đường vuông góc từ điểm đó đến mặt phẳng.

Hình chiếu vuông góc của điểm A lên mặt phẳng (P) là điểm H sao cho đường thẳng AH vuông góc với mặt phẳng (P).

Tại đây, chúng tôi còn chia sẻ thêm những công thức tính thể tích hình thang, nếu bạn có nhu cầu thì đừng bỏ qua nha.

Tìm tọa độ hình chiếu vuông góc của điểm lên mặt phẳng

Để xác định được tọa độ hình chiếu vuông góc của điểm H dựa trên mặt phẳng P ta sẽ thức hiện các bước như sau:

• Bước 1: Viết phương trình mặt phẳng P chứa điểm A và vuông góc với d.
• Bước 2: Áp dụng công thức tính khoảng cách từ điểm đến mặt phẳng.
• Bước 3: Tìm tọa độ của điểm H và tính khoảng cách từ H đến mặt phẳng P.

Cách tính toán tọa độ hình chiếu vuông góc của điểm lên mặt phẳng

Để tính toán tọa độ của điểm H là hình chiếu vuông góc của điểm M lên mặt phẳng P.

• Bước 1: Xác định phương trình mặt phẳng P là (α): x + y + z = 0, để tính hình chiếu của điểm M lên đó.
• Bước 2: Tìm tọa độ của điểm M là A(3, 2, -1).
• Bước 3: Tính tọa độ hình chiếu vuông góc của điểm H lên mặt phẳng P, để tính được chính xác tọa độ H cần tìm điểm trên mặt phẳng P sao cho đường thẳng đi qua điểm M và vuông góc với mặt phẳng (P).
• Bước 4: Tính giao điểm giữa đường thẳng và mặt phẳng.
• Bước 5: Tìm tọa độ giao điểm của điểm H.

Bài tập ví dụ: Tìm giao điểm của đường thẳng d và mặt phẳng P là tọa độ điểm H, như vậy là ta sẽ có hình chiếu vuông góc của điểm M lên mặt phẳng P.

Tọa độ điểm H là hình chiếu vuông góc của hệ phương trình sau:

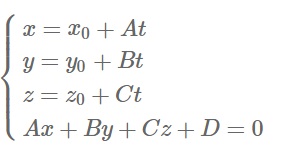
Ngoài những cách giải trên bạn cũng có thể tham khảo cách giải của thầy Đặng Thành Nam trong bài viết sau:

Ứng dụng của hình chiếu

Hình chiếu vuông góc của một điểm lên mặt phẳng được sử dụng trong nhiều lĩnh vực khác nhau như đo đạc và khảo sát, thiết kế xây dựng, toán học,...

• Đo đạc và khảo sát: Hình chiếu vuông góc được áp dụng nhiều trong đo đạc đất đai, nó giúp xác định vị trí và khảo sát các vùng đất đai cần xây dựng phù hợp với các bản thiết kế công trình.
• Thiết kế và xây dựng: Việc tính hình chiếu vuông góc của điểm lên trên mặt phẳng giúp cho việc thiết kế và tính toán các vật liệu xây dựng tại các hạng mục của công trình trở nên dễ dàng hơn. Hình chiếu đóng vai trò quan trọng trong việc tạo ra các bản vẽ kiến trúc giúp cho các kiến trúc sư trình bày và chia sẻ ý tưởng thiết kế với khách hàng.
• Toán học và khoa học máy tính: Việc tính toán hình chiếu vuông góc giúp giải các bài tập hình học không gian, nó cũng được sử dụng trong khoa học máy tính để tính toán các dữ liệu.
• Trong lĩnh vực địa lý: Hình chiếu được sử dụng để tạo ra các bản đồ và hình ảnh về bản đồ hỗ trợ trong quá trình nghiên cứu địa lý, hình chiếu dùng để xác định các hệ thống tọa độ địa lý như hệ tọa độ UTM. Nó cũng được sử dụng để biến đổi dữ liệu từ hệ tọa độ này sang một hệ tọa độ khác và tích hợp dữ liệu từ nhiều nguồn khác nhau. Hình chiếu cũng được sử dụng để phân tích dữ liệu địa lý và tạo ra các bản đồ, với những thông tin trực quan dễ hiểu về những dữ liệu địa lý.

Trong toán học, Cách tính phần trăm cũng là một kiến thức quan trọng, các bạn hãy cùng tìm hiểu thêm trong bài viết được chia sẻ tại đây nha.

Bài tập vận dụng

Bài tập 1: Cho đường thẳng d có phương trình x - y = 0 và điểm M là (1; 3), tìm hình chiếu vuông góc của điểm M lên mặt phẳng d?

Giải:

Gọi H (a;b) là hình chiếu vuông góc của M trên d.

Do H thuộc d nên a - b = 0 (1)

Ta có: MH→(a - 1; b - 3).

Đường thẳng MH vuông góc với d nên MH→ cùng phương với nd→ (1; -1)

⇒ ⇔ -a + 1= b - 3 hay a + b = 4 (2)

Từ (1) và (2) ta có hệ phương trình :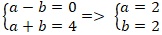

Từ đó ta suy ra tọa độ điểm H là (2; 2).

Bài tập 2: Cho đường thẳng d: 5x + y - 6 =0 và điểm (1; 1), tính hình chiếu vuông góc của điểm A trên mặt phẳng d.

Giải:

Thay tọa độ điểm A vào phương trình đường thẳng d, ta có hệ phương trình sau:

5.1 + 1 - 6 = 0 ⇒ (1; 1).

Suy ra điểm A thuộc đường thẳng d nên hình chiếu trên đường thẳng d là của điểm A.

Trên đây Mosflyvn.com đã chia sẻ cách xác định hình chiếu vuông góc của điểm lên mặt phẳng trong việc tính toán các bài toán hình học không gian, để việc tính toán được chính xác bạn cần xác định tọa độ và cách tính tọa độ hình chiếu.

Các bạn hãy ghé thăm chuyên mục Khám phá của chúng tôi thường xuyên để không bỏ lỡ bất kỳ bài viết nào nhé.